EPIDEMIOLOGY MODELING
Epidemiological models of infectious diseases have greatly improved our understanding of how they spread through a population. They also play an increasingly important role in the formation of public health policies. Broadly speaking we are interested in the role of interventions (e.g. vaccines, prophylactic use of treatments) to mitigate or halt the impact of infectious diseases.
Research
Background
Mathematical modeling has contributed greatly over the years to the analysis of the population-level effects of interventions - especially vaccination - against infectious agents. The earliest example is Daniel Bernoulli's smallpox model that estimated the effects of variolation (a precursor to the concept of vaccination) on population mortality rates, back in 1760s. Bernoulli's work was the first quantitative demonstration of the potential benefits of individual preventive measures on the overall health of the population. The development of Kermack and McKendrick's classical SIR mathematical model - an ODE model with equations for those 's'usceptible to, 'i'nfected with, and 'r'ecovered from, a disease - in 1927 constitutes without a doubt a hallmark in infectious disease research. The SIR model and its generalizations have been extremely useful to understand the dynamics of disease spread, the effects of herd immunity on disease prevalence and the minimum levels of vaccination coverage required to eradicate specific endemic diseases.
Approach
The techniques we employ include network theory and simulation, which lend greater realism to models, and compartmental modeling, which - while less realistic (based on homogeneous mixing assumptions) - is more analytically tractable. we am also interested in developing multi-scale models, nesting within-host dynamics within an epidemic model. Such models can be used to gain insight into pathogen strain diversity and emergence of drug-resistant infections.
Influenza in Vancouver
While a part of Dr. Pourbohloul's group at the BC Centre for Disease Control (BCCDC) in Vancouver, Canada, Conway developed a population-dynamics model of influenza spread in the Greater Vancouver Regional District. The model incorporated information from the Vancouver Contact Network, developed by colleagues at the BCCDC, into a structured compartmental model, lending the realism obtained via network modeling to a more computationally efficient framework. We used this model to make policy recommendations to the BC Health Minister, for example with regards to antiviral use, during the 2009 pH1N1 epidemic.
We also used this model to investigate the interplay between vaccination targeting strategies, and vaccine distribution timing. Much public-health emphasis is placed in vaccine targeting strategies: how should the vaccines be best distributed to limit adverse outcomes such as flu-related mortality? What age groups should be prioritized? Structured mathematical models have yielded guidance on this issue ((Medlock & Galvani 2009, Science(325):1705-1708 link). However models frequently assess the efficacy of vaccines distributed in advance of an epidemic, which is not always realistic. For the pH1N1 epidemic the vaccine was only available in Canada starting October 26, after the epidemic peaked! Do the same vaccine targeting strategies make sense?
Nope.
Or, more precisely, our modeling results suggest that they don't.
We used our model to evaluate the reduction in incidence and mortality resulting from different age-specific targeting strategies: (1) "Actual," the reported age distribution on vaccines in the pH1N1 epidemic in Vancouver; (2) "Uniform," the distribution of the same number of doses evenly across all age groups; and (3) "Parents and children (PC)," the strongly supported strategy (Medlock & Galvani 2009) wherein school-age children and their parents only are vaccinated. School-age children are thought to be the most significant spreaders of the flu - notice in Figure 1, the epidemic peaks sooner for 5-17 year-olds than for any other group! Finally, since the population fraction of children and their parents is less than the vaccinated population fraction from the "Actual" strategy, we consider a fourth strategy, (4) "Parents and children plus (PC+)," where after parents and children are vaccinated the remaining balance of doses are distributed to the rest of the population proportionally according to the "Actual" strategy.
We then examine incidence and mortality reduction resulting from an 8-week campaign using any of these strategies varying the start date. Results are shown in Figure 1.
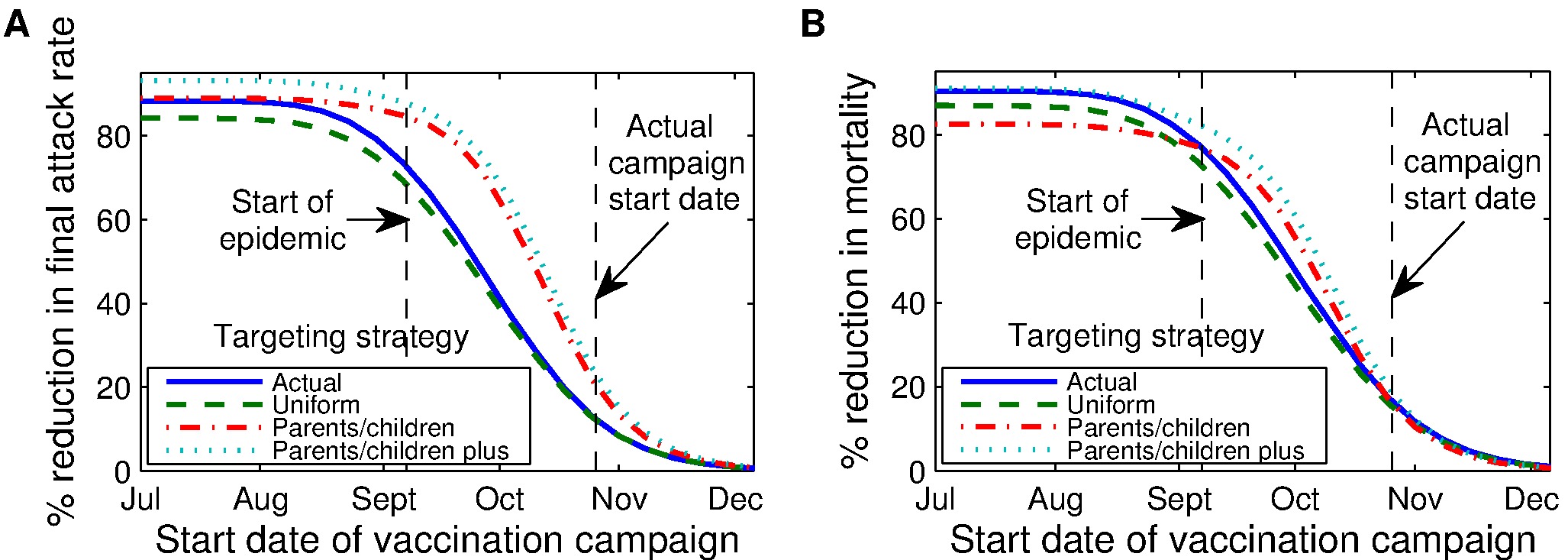 |
- * For campaigns initiated before or early into the epidemic, PC and PC+ strategies are best at reducing the final attack rate (cumulative incidence at the end of the epidemic).
- * However, the Parents and Children only strategy - initiated before the epidemic - actually leads to higher mortality rate. This is because the elderly, who represent a less significant group with regards to transmitting the disease, have the highest flu-mortality rates. And under the PC strategy they are left completely unprotected.
- * For campaigns initiated late in the epidemic, as was the case in 2009, the resulting % reduction in final attack rate across strategies is small, and the differences in % reduction of mortality are very small, almost imperceptible.
With pandemic influenza, it is quite possible that a vaccine may only become available late into the epidemic. A lot of money and effort goes into vaccine targeting strategies, which are very effective if vaccines are distributed before or early in an epidemic. However for campaigns initiated later, our modeling predictions suggest that targeting strategies would best be put aside: getting needles in arms, anybody's arms, should be the priority instead.
For more details including a discussion of campaign duration and distribution rates and a sensitivity analyses, please see:
J.M. Conway et al., "Vaccination against 2009 pandemic H1N1 in a population dynamical model of Vancouver, Canada: timing is everything," BMC Public Health, 11, 932 (2011). link
CURRENT WORK
The previous study shows that the optimal strategy changes as the epidemic proceeds. But we haven't determined what optimal targeting strategies are, nor how significant their impact will be.
Rachel Hoellman is currently working with me on that problem.