BROADLY SPEAKING...
We investigate viral infections and their interplay with therapy. While each viral infection is different, the beauty of applied mathematics and modeling is that we can use similar or related mathematics to gain insight into their dynamics.
Current and recent investigations include predicting antiviral drug resistance in flu infection, and optimal curative antiviral regimen with respect to drug resistance prevention; theoretical analysis of hepatitis C dynamics under therapy. We are interested in applying modeling and techniques to the viral infection of your choice, but for now our primary focus is HIV.
WITHIN-HOST HIV VIRAL DYNAMICS PROBLEMS
Modeling of viral dynamics has been very successful in gaining insight into HIV infection. I am interested in understanding within-host viral dynamics in individuals, with emphasis on the interplay between infection and therapy:
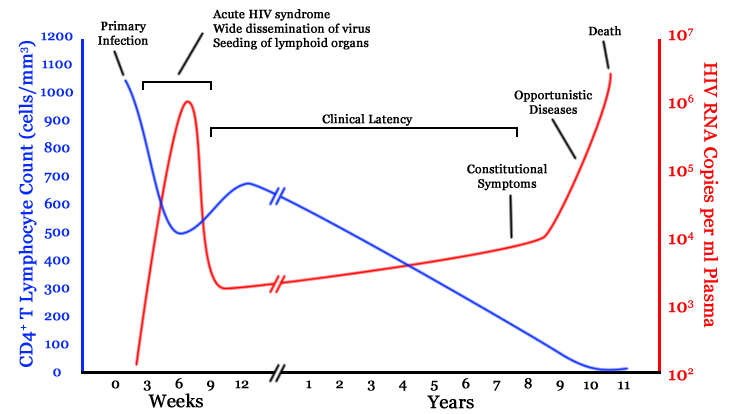
(1) The events that occur between virus exposure and development of symptomatic disease. These are poorly understood and often difficult to study in patients. However, these events are critically important in determining disease outcomes, as well as the effectiveness of drugs and later immune responses. Interventions (e.g. HIV treatments) are used to prevent HIV infection at this stage, with pre-exposure prophylaxis (taking drugs in advance of exposure) gaining FDA approval in 2012. But optimal use remains uncertain.
(2) Dynamics of treated chronic HIV infection. Treatments for HIV are of very high quality, and while a patient is on treatment their infection may be undetectable. However, typically an interruption in treatment yields once-again detectable infection: treatments are not a cure. But, why not? What are mechanisms of disease persistence in spite of very effective treatments? And what role do they play in emergent drug resistance?
(3) Typically an interruption in treatment yields once-again detectable infection, i.e. viral rebound, within a few weeks. But not always! The Mississippi baby's viral rebound took 27 months, and the French VISCONTI cohort patients have been off treatment with no rebound for years. Why is rebound delayed? Can we create conditions for infection control with NO therapy?
Background & Approach (with HIV infection as model system)
Background
Viruses replicate by infecting a hosts' healthy cells and hijacking those cells' genetic machinery to make copies of itself. HIV infects primarily immune system cells, in particular helper T-cells.
 |
 |
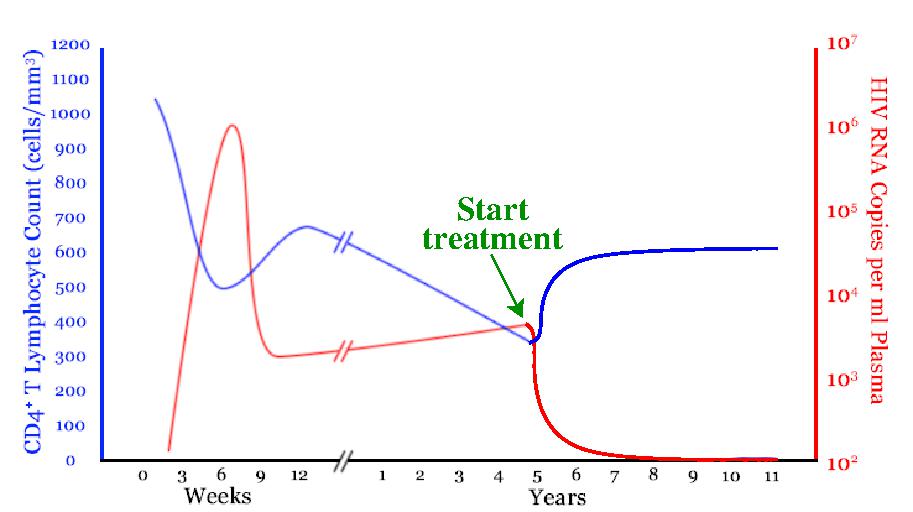 |
Starting with analyses of Ho and Perelson (1995 Nature, 373:123-6), using differential equation models fit to data to estimate viral production and clearance rates, we have relied on mathematical models to gain insights into HIV infection. While deterministic (differential equation) models remain the standard, stochastic modeling approaches have gained momentum as well (for example, see Tan and Wu, "Deterministic And Stochastic Models of AIDS Epidemics And HIV Infections with Interventions," World Scientific Pulblishing (2005)).
Approaches
Basic viral dynamics models are deterministic models examining the interplay between virus and host cells. One approach I am currently using to test hypotheses with regards to immune system activation and its role in HIV infection progression is building models and fitting them to data. We use statistical tools to evaluate goodness of fit and whether our hypotheses are consistent with data.
However, during the earliest stages of HIV infection - and in chronically infected, treated patients - viral and infected cell populations can be very low. In these regimes a deterministic approach, focusing on average behaviour, is inappropriate. We utilize instead a non-traditional, stochastic approach: multi-type, continuous-time branching formulations. Loosely speaking we consider coupled birth-and-death processes on different cell types.
Such systems can be described by differential Chapman-Kolmogorov equations. From these equations, we can derive differential equations for the probability generating function and use a novel numerical technique to extract probability distributions over time for the different cell types. We can also use this formulation to investigate small-probability, large deviations from the mean viral load (viral blips), risk of infection after exposure to HIV virus, and infection clearance times. These clinically important quantities are inaccessible using traditional ODE formulations.